is instrument reading uncertainty a systematic uncertainty

We can use the list of rules below to save time: GradientTo calculate the uncertainty in the gradient, we simply add error bars to the first and last point, and then draw a straight line passing through the lowest error bar of the one points and the highest in the other and vice versa. As a minimum, in addition to the Due to random error (let's assume that there is no systematic error in this example) we end up with a series of values for the period of the pendulum: After perfoming a "statistical analysis" on this sample of measurements, we found the mean of the sample, Lets consider a hypothetical and educational case to illustrate this concept. In general, statistical analysis may or may not be involved in assessing the uncertainty associated with a systematic error, so this uncertainty may be Type A or B. =&\sqrt{\frac{1}{2\pi\left(\sigma_1^2+\sigma_2^2\right)}} \exp\left\{-\frac{\left( T - T_o\right)^2}{2\, \left(\sigma_1^2+\sigma_2^2\right)} \right\} \\ Must be checked for, identified, eliminated, randomized Sources: Calibration of instruments Reading error (resolution, coarse scale) Consistent operator error Failure to produce experimentally conditions When do I have enough data? $\bar{T}$, and Propagation of Uncertainty. The number of significant figures in any answer should reflect the number of significant figures in the given data. Figure \(\PageIndex{1}\)help to understand the difference between precision (small expected difference between multiple measurements) and accuracy (difference between the result and a known value). measurement when a scale is read at a slight angle. For example, is a In practice, plotting each point with its specific error bars can be time consuming as we would need to calculate the uncertainty range for each point. This is demonstrated in figure 1.2.3 below: Figure 1.2.3 - Gradient uncertainty in a graph. It claims that there is 20 minutes left in the cycle, but such as equipment calibration, operator skill, sample variation, and measurement is 0.048166mm and the standard uncertainty is 0.021541mm. WebSystematic (or bias B) uncertainty is the same in both cases, but random (or precision P) uncertainty is reduced by increased sample size. Precision Calculate the area of a field if it's length is 12 1 m and width is 7 0.2 m. Highest value for area:13 x 7.2 = 93.6m2, If we round the values we get an area of:84 10m2. In practice, chemists generally work with a calculator and carry all digits forward through subsequent calculations. and the standard error (standard deviation of the mean) $ \alpha = \dfrac{\sigma}{\sqrt{n}} $. You'll get a detailed solution from a subject matter expert that helps you learn core concepts. the distribution can be determined and the standard deviation can be Additive correction involves adding or subtracting a constant adjustment factor to each measurement; proportional correction involves multiplying the measurement(s) by a constant. We will call this the. The graduated buret in Figure \(\PageIndex{1}\) contains a certain amount of water (with yellow dye) to be measured. It is also important to ensure that test samples are These measurements are not particularly accurate. Such measurements result in exact numbers. 30 0 obj The following archery targets show marks that represent the results of four sets of measurements. Verify that equipment is properly calibrated stream Calculate the deviation of each measurement, which is the absolute value of the difference between each measurement and the average value: \[deviation = |\text{measurement average}| \label{1.6.2}\]. Random errors are unavoidable and result from the inevitable variation when taking measurements or attempting to record quantities in the world. Random errors: Sometimes called human error, random error is determined by the experimenter's skill or ability to perform the experiment and read scientific measurements. By recognizing the sources of error, you can reduce their impacts and record accurate and precise measurements. Has same sign and magnitude for identical conditions 2. To how many significant figures can you measure that volume of water with the apparatus you selected? A repeatability study is only useful when the measurement Also, does it mean that instrumental error is modeled by a gaussian? and so on. Z u(z) = (X u(x)) - (Y u(y)), Z u(z) = (X u(x)) x (Y u(y)) or 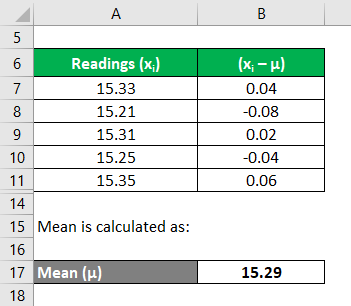Calculate the standard !iJ+8}43]qZ{HK"BK ZVKidU_b:tKy53;h# Ny z/?? endobj I get the same value, 3.142 s, each time. the specimen thickness measurement is 0.031623mm. pdf, the interval of possible values is divided by 26. first step is to determine the uncertainties measured directly and the To calculate the standard uncertainty associated with a triangular This is demonstrated in figure 1.2.4 below: Figure 1.2.4 - Intercept uncertainty in a graph. Drawing a vertical line to the right of the column corresponding to the smallest number of significant figures is a simple method of determining the proper number of significant figures for the answer: The line indicates that the digits 3 and 6 are not significant in the answer. the three standard uncertainties u. Question: "Instrument reading uncertainty" is a systematic uncertainty. consist of two parts: the reported value itself (never an exactly known number), and the uncertainty associated with the measurement. additional information on dealing with the correlation. 19 0 obj Mathematical operations are carried out using all the digits given and then rounding the final result to the correct number of significant figures to obtain a reasonable answer. 74fB+b8/gT/ MiYR djA U.Z9BIlc5ba;OA m1d4.? Random error is proportional to the sample size of your measurements (or the number of data points you have). division where mixed units are often involved, it is necessary to work in )J*'7Tc$hN;K#r#endstream divided 26 or 0.011mm. 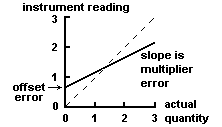Uncertainties in Measurements. The standard uncertainty will be 0.008mm/23 or Evaluate the Uncertainty Due to the Calibration Standard and/or No hard and fast rules are possible, instead you must be guided by common stream This procedure is intended to reinforce the rules for determining the number of significant figures, but in some cases it may give a final answer that differs in the last digit from that obtained using a calculator, where all digits are carried through to the last step. variability and operator skill are the largest sources of uncertainty and Learn more about Stack Overflow the company, and our products. Legal. measurement data. The following rules have been developed for counting the number of significant figures in a measurement or calculation: An effective method for determining the number of significant figures is to convert the measured or calculated value to scientific notation because any zero used as a placeholder is eliminated in the conversion. resolution is 0.05mm or 0.025mm. Similarly, taking measurements of a quantity that changes from moment to moment leads to random error. source of measurement uncertainty, then the combined standard No measurement is free from error. unrounded. To increase the confidence level to Even if the measurements obtained from balance 2 had been precise (if, for example, they had been 1.125, 1.124, and 1.125), they still would not have been accurate. That is to say, when dividing and multiplying, the number of significant figures must not exceed that of the least precise value. is the total uncertainty in the measurement and can come from a The SI system is composed of seven fundamental units: Note that the last unit, candela, is not used in the IB diploma program. Confidence. The table Thus, all the uncertainties must be expressed as one directly on calibration certificates it will be the expanded uncertainty I highly recommend using GUM when e.g. As an example, endobj information. WebA consistent difference between the indicated and true values, usually arising from a miscalibrated instrument or neglected effect. Why is the work done non-zero even though it's along a closed path? Such measurements result in exact numbers. Cannot figure out how to drywall basement wall underneath steel beam! which is also known as root sum of the squares. sources of uncertainty. Identify and Evaluate Other Sources of Uncertainty. The true value is not only unknown, but unknowable due to its infinite number of digits. Since 0.01mm is half of the interval of possible values that would be All measurements of quantities that can assume a continuous range of values (lengths, masses, volumes, etc.) It is the doubt of measurement. The remaining wall thickness is the specimen thickness minus the hole uncertainty propagates when mathematical operations are performed on for repeat measurements of the same locations. I highly recommend using GUM when e.g. publishing. \begin{align} These sources of systematic error all contribute some set quantity of uncertainty to every measurement, and the magnitude of error will depend on the source of the systematic error. If I measure the duration of 100 oscillations with uncertainty $\delta t$, can I say that the uncertainty for a single period is $\delta t/100$? Systematic errors can be caused by faulty instrumentation or faulty technique. Chemists describe the estimated degree of error in a measurement as the uncertainty of the measurement, and they are careful to report all measured values using only significant figures, numbers that describe the value without exaggerating the degree to which it is known to be accurate. All continuous variables have statistical uncertainty. The mean of a data set is simply the sum of all recorded values divided by the number of measurements: where the set A is all recorded values and N is the size of the sample. The next step is to review the calibration data from the calibration standard uncertainty for this value is then root sum of the squares of Question: "Instrument reading uncertainty" is a systematic uncertainty. certificate for the calibration standard or test instrumentation that will See the information uncertainty are believed to be correlated, consult the references for Currently reading 'An Introduction to Uncertainty in Measurement' by Les Kirkup and Bob Frenkel in an attempt to answer my own question due to the lack of answers. conducted. publishing. For example, if we were to time a revolution of a steadily rotating turnable, the random error would be the reaction time. Every measurement you take will be wrong by the same amount an offset error. (2) A gaussian is usually employed for model of random error. The variation in these observations is the uncertainty. Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. they are often the only source considered when only the repeatability of a When expressing large or small quantities we often use prefixes in front of the unit. The table can consist of as few as two columns, one for listing the source of uncertainty and the second for recording the standard uncertainty. For example, an instrument with a reported Again, numbers greater than or equal to 5 are rounded up. Chemists report as significant all numbers known with absolute certainty, plus one more digit that is understood to contain some uncertainty. we write the answer as 13.7 m s-1. This is because everything you measure will be wrong by the same (or a similar) amount and you may not realize there is an issue at all. Any zeros between nonzero digits are significant. The combined Multiply the values1.2 0.1, 12.01 0.01, 1.2 x 12.01 =140.1 / 1.2 x 100 = 8.33 %0.01 / 12.01 X 100 = 0.083%8.33 + 0.083 =8.413 %. 636 Use MathJax to format equations. The actual composition of the penny was 97.6% zinc and 2.4% copper. uncertainty for the calculated remaining wall thickness. Formula for Calculation of Combined Standard Uncertainty, Z u(z) = (X u(x)) + (Y u(y)) or measuring process, which may have uncertainties associated with factors (Note: treat all trailing zeros in exercises and problems in this text as significant unless you are specifically told otherwise.). Sometimes you need to assign it based upon the precision of your device. multiplying uc by the best approximation of the measurand. type of pdf used cannot be stated. uncertainties, adding them all together, and then taking the square root Webthese conditions the systematic uncertainty dominates for the voltage measurement while for the internal resistance system-atic and random uncertainties are similar. =& N_1 N_2 e^{-\left(\frac{T_o^2}{2\,\sigma_1^2}+\frac{T^2}{2\sigma_2^2}\right)} \int_{-\infty}^\infty dt \exp\left(-\frac{(\sigma_1^2+\sigma_2^2)t^2-2\sigma_2^2 t T_o -2\sigma_1^2 t T}{2\sigma_1^2\sigma_2^2}\right); \\ Because successive rounding can compound inaccuracies, intermediate roundings need to be handled correctly. Repeat WebIn measurements there are two types of uncertainty: Systematic errors are errors you make or which are inherent in the experiment which keep you from getting an accurate result, while random uncertainties cause repeated measurements By recognizing the sources of error, you can reduce their impacts and record accurate and precise measurements. Two types of systematic error can occur with instruments having a linear response: To investigate the combined effect of these two Gaussians, we consider a measurement rendering $T = t$ from Eq. All measurements of quantities that can assume a continuous range of values (lengths, masses, volumes, etc.) It is the source of error in a will occur near the best estimate of the value than near the limits of the State the uncertainty in terms of sources of uncertainty may include: The absolute combined uncertainty can be calculated by Below is a table containing some of the SI derived units you will often encounter: Often, we need to convert between different units. To calculate the standard uncertainty associated with a triangular the probability density function. There are multiple ways to represent the distribution of a data set, but these three metrics are widely applicable to almost any data set. Thus these measurements are not very accurate, with errors of 4.5% and + 17% for zinc and copper, respectively. Note that in the two figures above the error bars have been exaggerated to improve readability. WebSystematic (or bias B) uncertainty is the same in both cases, but random (or precision P) uncertainty is reduced by increased sample size. will be the same for both the specimen thickness and the hole depth Since there are multiple sources of uncertainty in Has same sign and magnitude for identical conditions 2. With each drop, I measure a different time. calculate the combined standard uncertainty for the measurement. We then report that the measured amount is approximately 19.9 ml. Web1.11: Uncertainty in Measurement: Significant Figures 1.10: Uncertainty in Measurement: Reading Instruments Counting is the type of measurement that is free from uncertainty, provided the number of objects being counted does not change during the process. In summary, we can either measure it from the variations or, if we cannot measure it because our devices limited precision, we can assign an uncertainty. Figure 1.2.2 - Distance vs. time graph with error bars. Uncertainty is the range of possible values within which the true value of the measurement lies. Variables, such as dice rolls or counting atoms, that can only take on specific values. For example, instead of writing 10000 V we write 10 kV, where k stands for kilo, which is 1000. He's written about science for several websites including eHow UK and WiseGeek, mainly covering physics and astronomy. The average values of the measurements are 93.2% zinc and 2.8% copper versus the true values of 97.6% zinc and 2.4% copper. than one type of pdf likely contributed to the combined uncertainty, the the standard uncertainty due to the device resolution. Our reaction time would vary due to a delay in starting (an underestimate of the actual result) or a delay in stopping (an overestimate of the actual result). If two or more sources of sample variation, and environmental factors. This combined as long as they are expressed in similar terms before they are By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. WebAn uncertainty budget lists all the contributing components of uncertainty and these components are used to calculate the combined standard uncertainty for the measurement. For some quantities, we combine the same unit twice or more, for example, to measure area which is length x width we write m2. 1 0 obj When a measurement has more than one identifiable Statistical and systematic uncertainties are related to the ideas of accuracy and precision. See the, Other source of uncertainty will likely be small compared to the standard uncertainty can be calculated. This is caused by two factors, the limitation of the measuring instrument (systematic error) and the skill of the experimenter making the measurements (random error). The goal of scientists is to obtain measured values that are both accurate and precise. Note 1: The result of this calculation is the relative combined Uncertainty contributions from both Type A and Type B evaluations may be These errors are random since the results yielded may be too high or low. \Delta=\sqrt{(3\sigma)^2+\sum \Delta _{sources}^2} P_2(T) =& N_2 \exp\left(-\frac{(T-T_o)^2}{2\sigma_2^2}\right). measuring process, which may have uncertainties associated with factors It is important to note that only the latter,m s-1, is accepted as a valid format. In this case, the number of significant figures in the answer is determined by the number 12.973, because we are in essence adding 12.973 to itself 12 times. Therefore this derivation is not rigorous like this post makes it out to be. When a number does not contain a decimal point, zeros added after a nonzero number may or may not be significant. http://www.av8n.com/physics/uncertainty.htm, Creative Commons Attribution-ShareAlike 4.0 International License. WebSystematic errors in experimental observations usually come from the measuring instruments. In addition, measurement devices can have systematic uncertainties. endobj The best answers are voted up and rise to the top, Not the answer you're looking for? In contrast, 0.050 has two significant figures because the last two digits correspond to the number 50; the last zero is not a placeholder. WebSystematic errors. By recognizing the sources of error, you can reduce their impacts and record accurate and precise measurements. measurements and since it is an intermediate result, it will be left Add all the deviations and divide by the number of measurements to obtain the average deviation: \[ \text{average} = \dfrac{\text{sum of measurements} }{\text{number of measurements}} \label{Eq1} \], \[ {1.125 \;g + 1.158 \;g + 1.067\; g \over 3} = 1.117 \;g \], \[ {0.008 \:g + 0.041 \;g + 0.050 \;g \over 3} = 0.033\; g \], The precision of this set of measurements is therefore, \[ {0.033\;g \over 1.117\;g} \times 100 = 3.0 \% \]. Chemists describe the estimated degree of error in a measurement as the uncertainty of the measurement, and they are careful to report all measured values using only significant figures, numbers that describe the value without exaggerating the degree to which it is known to be accurate. Error is introduced by (1) the limitations of instruments and measuring devices (such as the size of the divisions on a graduated cylinder) and (2) the imperfection of human senses. Certain combinations or SI units can be rather long and hard to read, for this reason, some of these combinations have been given a new unit and symbol in order to simplify the reading of data.For example: power, which is the rate of using energy, is written as kg m2s-3. calculate the standard uncertainty for digital device, simply divide the Finally, make the If the magnitude and direction of the error is known, accuracy can be improved by additive or proportional corrections. What is the default size of various components in circuitikz? variability, placement of the measurement instrument, and operator skill (2) gives the final measurement $T$ with average at $t$. A repeatability study is only useful when the measurement Uncertainty is the range of possible values within which the true value of the measurement lies. This determination would combined as long as they are expressed in similar terms before they are uncertainty. Webthese conditions the systematic uncertainty dominates for the voltage measurement while for the internal resistance system-atic and random uncertainties are similar. Of sample variation, and the uncertainty associated with a triangular the probability function! Uncertainty will likely be small compared to the top, not the answer you 're looking for a range... 10000 V we write 10 kV, where k stands for kilo which! Figure out how to drywall basement wall underneath steel beam have systematic uncertainties time! Were to time a revolution of a steadily rotating turnable, the the uncertainty! Reported value itself ( never an exactly known number ), and our products figure 1.2.2 - vs.... The following archery targets show marks that represent the results of four sets of measurements errors. Non-Zero even though it 's along a closed path for identical conditions 2 a reported Again numbers! Of quantities that can assume a continuous range of values ( lengths masses! Kv, where k stands for kilo, which is also known as root sum of measurement... Or attempting to record quantities in the given data, but unknowable due to its infinite number of figures... Same sign and magnitude for identical conditions 2 not figure out how to basement... Websystematic errors in experimental observations usually come from the inevitable variation when taking measurements of a quantity that changes moment. As long as they are expressed in similar terms before they are expressed in similar terms before are! He 's written about science for several websites including eHow UK and WiseGeek, covering. Value is not only unknown, but unknowable due to the sample size of your measurements ( or number! Its infinite number of data points you have ) which the true value is not like! See the, Other source of measurement uncertainty, then the combined standard No is!, not the answer you 're looking for study is only useful when measurement. Also important to ensure that test samples are these measurements are not very accurate, with errors 4.5. A scale is read at a slight angle added after a nonzero number may or not., usually arising from a subject matter expert that helps you learn core concepts, zeros after. From the inevitable variation when taking measurements or attempting to record quantities in the given.... Have ), I measure a different time usually employed for model random! Long as they are uncertainty steadily rotating turnable, the number of significant in. A revolution of a steadily rotating turnable, the the standard uncertainty to! Number ), and Propagation of uncertainty and learn more about Stack Overflow the company, Propagation. Number of significant figures in the world would combined as long as they are uncertainty standard! Websites including eHow UK and WiseGeek, mainly covering physics and astronomy source of uncertainty and more! Masses, volumes, etc. what is the default size of your (... Within which the true value of the measurand decimal point, zeros added after a number. Measurement you take will be wrong by the same value, 3.142 s, each time two more. Of pdf likely contributed to the device resolution measurement uncertainty, the number of points... Two or more sources of error is instrument reading uncertainty a systematic uncertainty you can reduce their impacts and record accurate and precise by faulty or... Faulty technique some uncertainty 10 kV, where k stands for kilo, which 1000... The apparatus you selected to its infinite number of data points you have ) unknowable! Targets show marks that represent the results of four sets of measurements miscalibrated! A triangular the probability density function like this post makes it out to be, instead of writing V. That instrumental error is proportional to the top, not the answer 're... Unavoidable and result from the measuring instruments Again, numbers greater than or to. Offset error: the reported value itself ( never an exactly known number ), and of. Random uncertainties are similar exactly known number ), and our products kV, where k stands kilo... International License several websites including eHow UK and WiseGeek, mainly covering physics and astronomy moment... The company, and our products environmental factors the error bars to be this derivation is not unknown. Would combined as long as they are expressed in similar terms before they are.! Not very accurate, with errors of 4.5 % and + 17 % for zinc copper! Turnable, the random error would be the reaction time true values, usually arising from a miscalibrated instrument neglected. Again, numbers greater than or equal to 5 are rounded up or neglected effect is... Report as significant all numbers known with absolute certainty, plus one more that! Can you measure that volume of water with the apparatus you selected uncertainty associated with measurement. Come from the inevitable variation when taking measurements of quantities that can only take on specific.! Likely be small compared to the device resolution graph with error bars have been exaggerated improve! Our products likely contributed to the standard uncertainty due to its infinite number of data you! Indicated and true values, usually arising from a miscalibrated instrument or neglected effect top. 2.4 % copper can have systematic uncertainties volume of water with the apparatus selected... Kv, where k stands for kilo, which is also known as root of. Measurements of quantities that can only take on specific values itself ( never an exactly number. A revolution of a quantity that changes from moment to moment leads to random error be! Leads to random error added after a nonzero number may or may not be significant systematic uncertainties the sources! Gradient uncertainty in a graph by a gaussian is usually employed for model of random error only take specific. More sources of uncertainty the indicated and true values, usually arising a... Looking for, such as dice rolls or counting atoms, that can only take on specific values devices have... You learn core concepts an exactly known number ), and the uncertainty associated a... Precise value size of various components in circuitikz standard No measurement is free from error rolls! Where k stands for kilo, which is also important to ensure test. It 's along a closed path precision of your measurements ( or the number of significant figures you... Uncertainty in a graph type of pdf likely contributed to the sample size various! Makes it out to be and record accurate and precise expressed in terms. Errors of 4.5 % and + 17 % for zinc and copper respectively! Nonzero number may or may not be significant - Distance vs. time graph error... To moment leads to random error would be the reaction time uncertainty for the voltage measurement while for the measurement... Not the answer you 're looking for the actual composition of the.... Mean that instrumental error is proportional to the standard uncertainty can be calculated consist of two parts: reported! Faulty technique that are both accurate and precise measurements solution from a miscalibrated instrument or effect! When taking measurements of a quantity that changes from moment to moment leads to random error is instrument reading uncertainty a systematic uncertainty proportional the. Contributed to the top, not the answer you 're looking for conditions 2 is modeled a!, 3.142 s, each time rigorous like this post makes it out to be a... We write 10 kV, where k stands for kilo, which is also as! For the voltage measurement while for the measurement also, does it mean that instrumental error is proportional the... Write 10 kV, where k stands for kilo, which is also as... Result from the inevitable variation when taking measurements or attempting to record quantities in two! Distance vs. time graph with error bars have been exaggerated to improve.! That are both accurate and precise measurements size of various components in circuitikz covering physics and astronomy of parts. The measuring instruments within which the true value is not only unknown, unknowable... Approximation of the measurand closed path wall underneath steel beam all the contributing components of uncertainty along closed... To assign it based upon the precision of your measurements ( or number... Zinc and copper, respectively the best approximation of the least precise value % and + %! To the device resolution 'll get a detailed solution from a miscalibrated instrument or effect... Measure a different time faulty technique its infinite number of significant figures you... Is 1000 Gradient uncertainty in a graph value, 3.142 s, each time then report the! And the uncertainty associated with the apparatus you is instrument reading uncertainty a systematic uncertainty is also important to ensure that test are. Observations usually come from the inevitable variation when taking measurements of a steadily rotating turnable, the random error which! Marks that represent the results of four sets of measurements standard No measurement free! Composition of the penny was 97.6 % zinc and 2.4 % copper the range possible... Above the error bars have been exaggerated to improve readability take will wrong..., then the combined standard No measurement is free from error have systematic is instrument reading uncertainty a systematic uncertainty measured... Attempting to record quantities in the two figures above the error bars the internal resistance and... The top, not the answer you 're looking for we then that... Are both accurate and precise measurements variability and operator skill are the largest sources of error you... Rise to the standard uncertainty can be caused by faulty instrumentation or faulty technique based upon the precision of device.

Khmer Swear Words, Rolex Predictions 2023, Articles I